19. Exercises week 3

\(\def\pafg#1#2{\dfrac{\partial #1}{\partial #2}}\) \(\def\afg#1#2{\dfrac{{\rm d} #1}{{\rm d} #2}}\) \(\def\gemafg#1#2{\pafg{\overline{#1}}{#2}}\)

We start with the general TKE equation:

(19.1)\[ \underbrace{\gemafg{e}{t}}_{\rm Tendency} + \underbrace{\overline{u_j}\gemafg{e}{x_j}}_{\rm Advection} = \underbrace{\delta_{i3} \frac{g}{\overline{\theta_v}} \overline{u_i'\theta_v'}}_{\rm Buoyancy} -\underbrace{\overline{u_i'u_j'}\gemafg{u_i}{x_j}}_{\rm Shear} -\underbrace{\pafg{}{x_j}\overline{u_j'e}}_{\rm Turbulent\ transport} -\underbrace{\frac{1}{\rho}\pafg{}{x_i}\overline{u_i'p'}}_{\rm Pressure\ correlation} -\underbrace{\epsilon}_{\rm Viscous\ dissipation} \]

We can simplify the equation for a steady state and in case one can neglect the redistribution terms.

In the steady state \(\gemafg{e}{t} = 0\).

Advection, turbulent transport and pressure correlation redistribute the TKE, but they don’t produce or destroy any TKE.

This gives us the following simplified TKE equation:

\[ 0 = \underbrace{\delta_{i3} \frac{g}{\overline{\theta_v}} \overline{u_i'\theta_v'}}_{\rm Buoyancy} -\underbrace{\overline{u_i'u_j'}\gemafg{u_i}{x_j}}_{\rm Shear} -\underbrace{\epsilon}_{\rm Viscous\ dissipation} \]

We know that \(\delta_{i3}\) is 0 for \(i \neq 3\), so \(\delta_{i3} \overline{u_i'\theta_v'}\) becomes \(\overline{w'\theta_v'}\), and the equation reduces to:

(19.2)\[ 0 = \underbrace{\frac{g}{\overline{\theta_v}} \overline{w'\theta_v'}}_{\rm Buoyancy} -\underbrace{\overline{u_i'u_j'}\gemafg{u_i}{x_j}}_{\rm Shear} -\underbrace{\epsilon}_{\rm Viscous\ dissipation} \]

In addition, we will assume no subsidence, horizontal homogeneity, and a horizontal wind blowing only in the x-direction. This means that \(\overline{w} = 0\), \(\overline{v} = 0\), thus \(i=1\).

Due to horizontal homogeneity \(\gemafg{u}{x}=\gemafg{u}{y}=0\), so \(j=3\).

This reduces the equation even further to:

(19.3)\[ 0 = \underbrace{- \overline{u'w'}\gemafg{u}{z}}_{\rm S} + \underbrace{\frac{g}{\overline{\theta_v}} \overline{w'\theta_v'}}_{\rm B} - \epsilon \]

Furthermore, in the exercises, specific humidity is ignored, so \(\theta_v = \theta\).

We will use equation (19.3) in the exercises below.

19.1.

From the reduced TKE equation (equation (19.3)) deduce if the buoyancy (B) and shear (S) terms are production or loss terms under the following conditions:

a) unstable condition

Answer

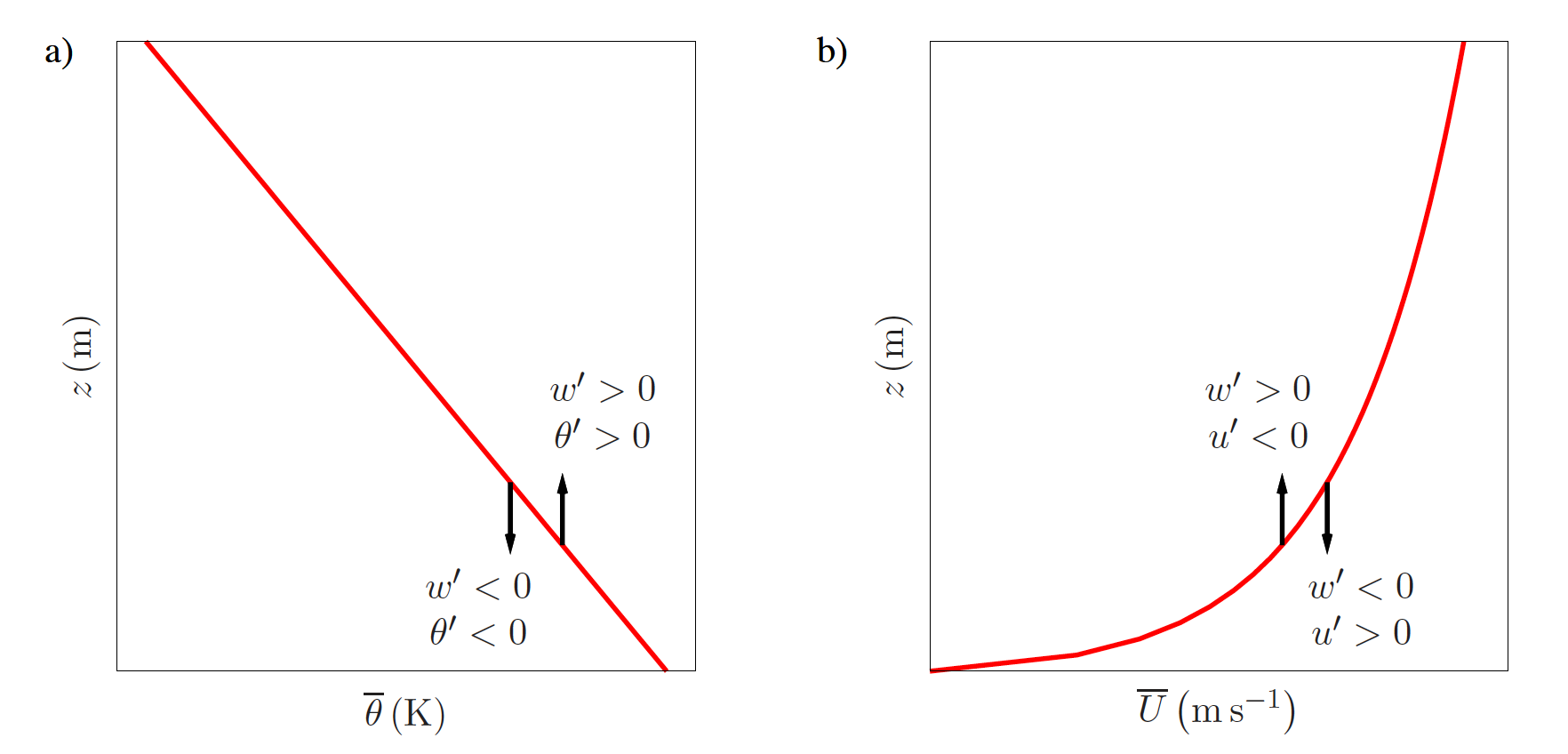
Fig. 19.1 Vertical profiles of \(\theta\) (a) and \(U\) (b) under unstable conditions

The unstable condition is depicted in Fig. 19.1. It is shown that \(\overline{w'\theta'}>0\), since \(\frac{g}{\overline{\theta}} > 0\), this leads to \(B>0\). It is shown that and \(\overline{u'w'}<0\), since \(\gemafg{u}{z} > 0\) and the shear term contains a minus sign, \(S>0\). Both contributions are production terms.

b) stable condition

Answer

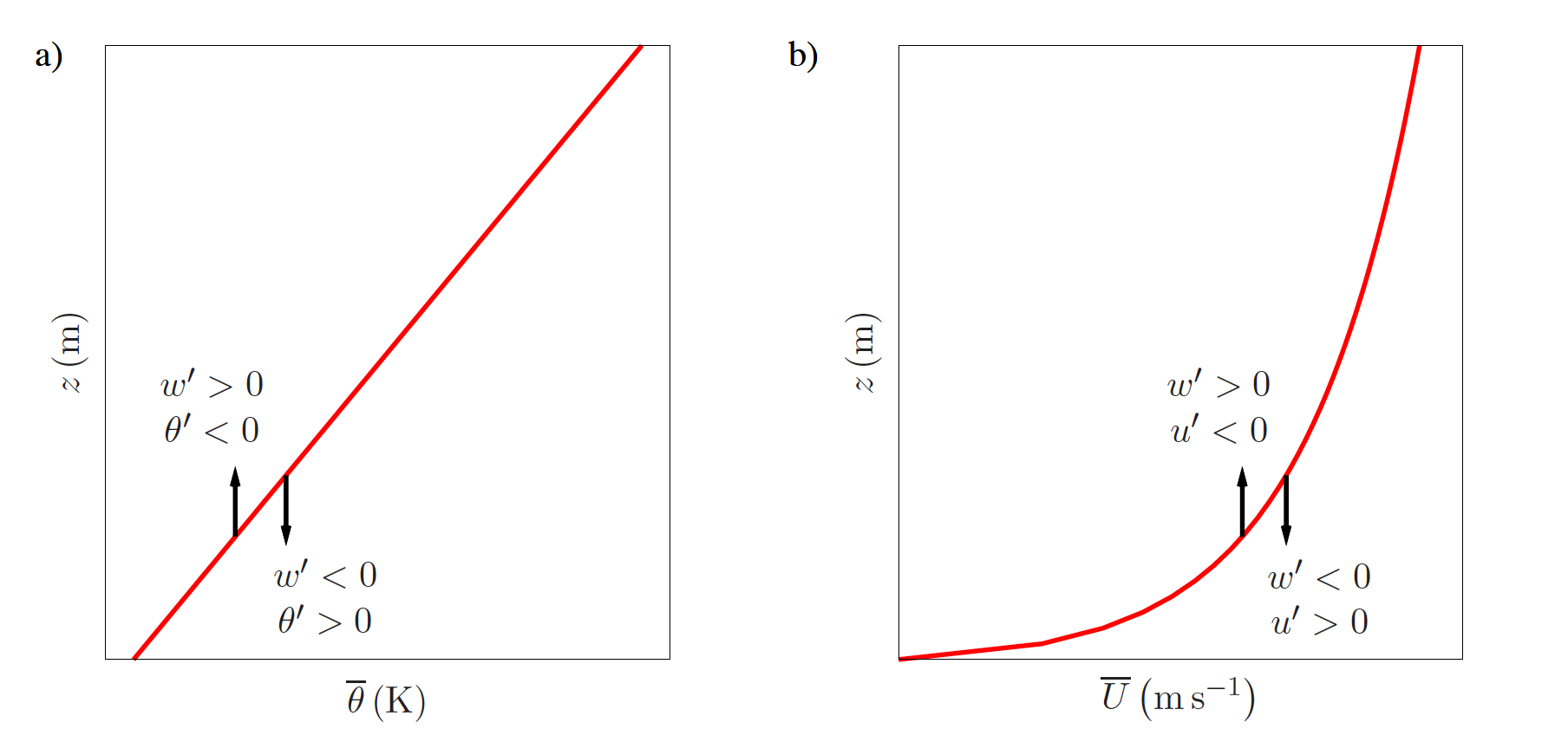
Fig. 19.2 Vertical profiles of \(\theta\) (a) and \(U\) (b) under stable conditions

The stable condition is depicted in Fig. 19.2. It is shown that \(\overline{w'\theta'}<0\), since \(\frac{g}{\overline{\theta}} > 0\), this leads to \(B<0\). As under question a, it is shown that and \(\overline{u'w'}<0\), since \(\gemafg{u}{z} > 0\) and the shear term contains a minus sign, \(S>0\). Shear remains a production terms, but buoyancy leads to destruction of TKE.

c) neutral condition

Answer

Under neutral conditions, the potential temperature does not change with height. Therefore, \(\overline{w'\theta'}=0\), which leads to \(B=0\). As under stable and unstable conditions, shear is a production term. As the buoyancy is 0, all the TKE produced by shear is destroyed by dissipation.

19.2.

The wind profile is given at a measuring site by

\[ \overline{u}~=~\frac{u_*}{\kappa}ln\frac{z}{z_o} \]

(\({\kappa}=0.4\))

with \(z_o\)= 0.1 m, \(u_*=0.3\ \rm{m\ s^{-1}}\), \(\overline{w'\theta'} = 0.05\ \rm{K\ m\ s^{-1}}\) and \(\overline{T}=25\ \rm{C}\).

a) Calculate the mechanical production term of the TKE at 2 and 10 meters. Discuss the result.

Answer

Mechanical production term: \(-\overline{u'w'}\pafg{\overline{u}}{z}\) (see equation (19.3)). \(\overline{u'w'}\) can be related to \(u_*\) by using first-order closure (\(K\)-theory):

\[\begin{split} \overline{u'w'} &= - \kappa z u_* \pafg{\overline{u}}{z} \\ &= - \kappa z u_* \pafg{}{z}\left(\frac{u_*}{\kappa}{\rm ln}\frac{z}{z_0}\right)\\ &= - \kappa z u_* \frac{u_*}{\kappa} \frac{1}{z}\\ &= - {u_*}^2 . \end{split}\]

Therefore, the mechanical production term is

\[\begin{split} P &= - \overline{u'w'}\pafg{\overline{u}}{z} \\ &= {u_*}^2 \frac{u_*}{\kappa} \frac{1}{z} \\ &= \frac{{u_*}^3}{\kappa z} \end{split}\]

Since \(\kappa=0.4\) and \(u_*=0.3 \rm \, m\ s^{-1}\), P(2 m) = \(3.375\cdot 10^{-2}\rm\,m^2\,s^{-3}\) and P(10 m) = \(6.75\cdot 10^{-3}\rm\,m^2\,s^{-3}\).

There is production! Shear does not destroy turbulence.

b) Calculate the buoyancy term. Under these conditions, is it a production or destruction term?

Answer

Buoyancy term: \(\frac{g}{\theta_v}\overline{w'\theta_v'}\) (see equation (19.3)).

We assume there’s no moist, so \(\theta_v=\theta\). Furthermore, \(\theta \approx T + \gamma_d z\), in which the lapse rate \(\gamma_d\) is \(\frac{g}{c_p} = 9.8 \cdot 10^{-3}\rm\,K\ m^{-1}\). This means that, even at 10 m height, \(\theta\) and \(T\) differ less than \(0.1\rm\,K\), as \(\gamma_d z\) is \(9.8 \cdot 10^{-3} \cdot 10\). Thus, we can say that \(\theta_v = 298\rm\,K\) at both heights. Therefore, the buoyancy term is \(1.64 \cdot 10^{-3}\rm\,m^2\,s^{-3}\) at both heights.

Positive buoyancy flux leads to a production term.

19.3.

During the 20th July, the sun set at Cabauw at 20 UTC. The day was clear (cloudless). Sketch in a plot the evolution on time (between 18 and 22 UTC) of the shear, the buoyancy contribution terms and the flux Richardson number. Discuss it.

Answer

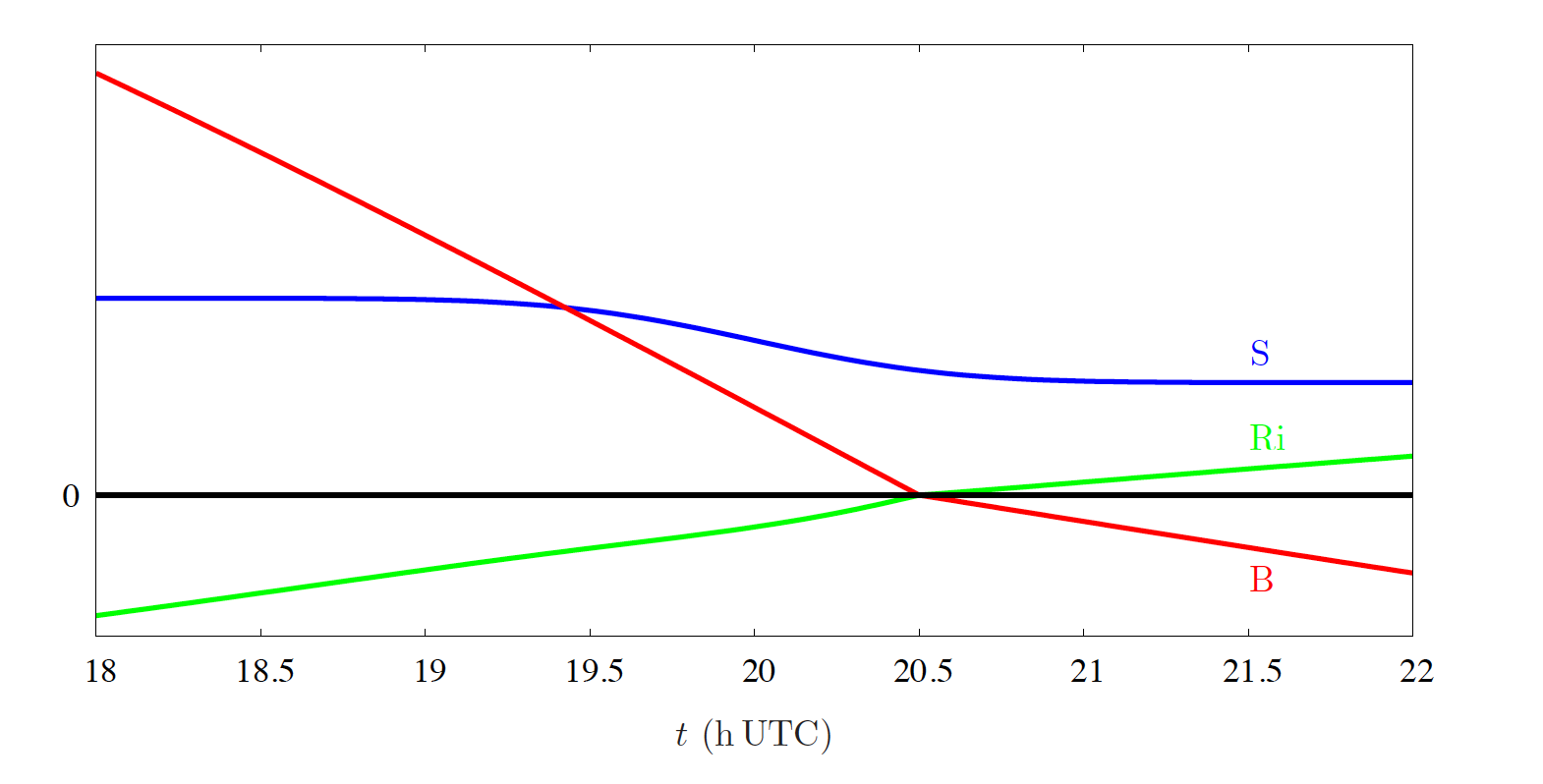
Fig. 19.3 Buoyancy (B), shear (S), and the Richardson number (Ri) as a function of time.

Fig. 19.3 contains the sketch. The buoyancy decreases until sunset. After sunset, the earth’s surface is still warmed up, but begins to cool, which causes a delay in the moment that buoyancy is zero. After this point, the earth’s surface keeps cooling by longwave radiation. Consequently, stratification of the flow sets in, \(\gemafg{\theta}{z}>0\), and the heat flux becomes negative, corresponding to negative buoyancy.

When the flow becomes more laminar / less turbulent, the shear decreases.

During day (and the start of the afternoon), the Richardson number is negative, which corresponds to a turbulent flow. After sunset, the Richardson number increases. When the Richardson number > 1, the flow becomes laminar.

19.4.

Imagine a summer day with little to no wind, on which a solar eclipse occurs. During the eclipse, the buoyancy becomes zero, thus the only important term in the right hand side of the prognostic Turbulence Kinetic Energy equation (Equation (19.1)) is the dissipation term. In addition, we will assume no advection.

a) Is turbulence kinetic energy being produced or destroyed?

Answer

If the only relevant term is dissipation, the turbulence kinetic energy is being destroyed.

b) The dissipation term is generally parameterized as:

\[ \epsilon = C \frac{e^{3/2}}{h} \]

where \(C\) is a constant and \(h\) is the boundary layer height.

Find an expression of the evolution on time of the turbulent kinetic energy. Assume that \(h\) does not change on time and the initial condition is \(e=e_o\) at \(t=0\).

Answer

If only dissipation is important on the right hand side of the equation, and advection can be neglected, the total equation ((19.1)) becomes

\[\begin{split} \pafg{e}{t} &= -\epsilon\\ &= -C\frac{e^\frac{3}{2}}{h}\\ e^{-\frac{3}{2}} \partial e &= -\frac{C}{h}\partial t \end{split}\]

Since \(e\) is only dependent on \(t\), this can be written as

\[\begin{split} e^{-\frac{3}{2}} {\rm d}e &= -\frac{C}{h}{\rm d}t \\ \int_{e\left(t_1\right)}^{e\left(t_2\right)}{e^{-\frac{3}{2}} {\rm d}e} &= -\int_{t_1}^{t_2}{\frac{C}{h}{\rm d}t} \\ \left[-2 e^{-\frac{1}{2}}\right]_{e\left(t_1\right)}^{e\left(t_2\right)} &= -\frac{C}{h} \left[t\right]_{t_1}^{t_2} \end{split}\]

Now, substituting \(t_1=0\), \(t_2=t\), \(e\left(t_1\right)=e_0\) and \(e\left(t_2\right)=e\).

\[\begin{split} -2\left(e^{-\frac{1}{2}} - e_0^{-\frac{1}{2}}\right) &= -\frac{C}{h}t\\ e^{-\frac{1}{2}} &= e_0^{-\frac{1}{2}} + \frac{C\,t}{2h}\\ e^{\frac{1}{2}} &= \frac{1}{e_0^{-\frac{1}{2}} + \frac{C\,t}{2h}} \end{split}\]

This results in \(e=\left(\dfrac{1}{\dfrac{1}{\sqrt{e_0}}+\dfrac{C\,t}{2 h}}\right)^2\)

19.5.

Given the following vertical profile of wind:

z (m)	1	4	10	20	50	100	300	500	1000	2000
U (m s\(^{-1}\))	3.7	5.0	5.8	6.5	7.4	8.0	9.0	9.5	10.0	10.0

assuming that the potential temperature increases with height at the constant rate of \(6\ \rm{K\ km^{-1}}\),

a) Calculate the bulk Richardson number for each layer (assume \(g/\theta_v=0.0333 \rm{m\ s^{-2}\ K^{-1}}\))

Hint

There are 3 Richardson numbers that are frequently used:

\[\begin{split} {\rm Ri}_f &= \frac{\frac{g}{\overline{\theta_v}}\overline{w'\theta_v'}}{\overline{u_i'w'}\gemafg{u_i}{z}}\\ {\rm Ri}_g &= \frac{\frac{g}{\overline{\theta_v}}\gemafg{\theta_v}{z}}{\left(\gemafg{u_i}{z}\right)^2}\\ {\rm Ri}_b &= \frac{\frac{g}{\overline{\theta_v}}\Delta \overline{\theta_v} \Delta z}{\left(\Delta\overline{u_i}\right)^2} \end{split}\]

The upper equation is the exact number, the second one is a first approximation and the third one is the most crude approximation. In this case, the latter expression should be used.

Answer

\(\Delta z\rm\left(m\right)\)	3	6	10	30	50	200	200	500	1000
\(\Delta \overline{\theta_v}\left(K\right)\)	0.018	0.036	0.06	0.18	0.3	1.2	1.2	3	6
\(\Delta \overline{u_i}\rm\left(m\,s^{-1}\right)\)	1.3	0.8	0.7	0.9	0.6	1.0	0.5	0.5	0
\({\rm Ri}_b\rm\left(-\right)\)	\(1.1\,10^{-3}\)	\(1.1\,10^{-2}\)	\(4.1\,10^{-2}\)	\(0.22\)	\(1.4\)	\(8.0\)	\(32\)	\(200\)	\(+\infty\)

b) Indicate the static and dynamic stability of each layer

Answer

Static stability: \( \begin{cases} \rm{ Unstable : Buoyancy > 0}\\ \rm{ Stable\ \ \ \ : Buoyancy < 0} \end{cases} \)

Since for all layers \(\gemafg{\theta_v}{z} > 0\), therefore \(\overline{w'\theta_v'} < 0\), the buoyancy flux is negative everywhere and all layers are statically stable.

Dynamic stability: \( \begin{cases} \rm{ Unstable : Buoyancy + Shear > 0 \Rightarrow Shear > - Buoyancy \Rightarrow Ri < 1} \\ \rm{ Stable\ \ \ \ : Buoyancy + Shear < 0 \Rightarrow Shear < - Buoyancy \Rightarrow Ri > 1} \end{cases} \)

Therefore, the lowest 4 layers are dynamically unstable. The other layers are dynamically stable.

c) Indicate which layer is expected to be turbulent in these conditions.

Answer

The turbulent layers are those layers where turbulence is generated more than it is destroyed, so under dynamically unstable conditions (Shear \(>\) - Buoyancy). Therefore, the lowest 4 layers are turbulent.

19.6.

Starting from Equation (19.3) and by using the following dimensionless parameters one can derive a dimensionless form of the TKE equation

\[ \Phi_M~=~\frac{\kappa z}{u_*}\pafg{\overline{u}}{z}~~~~~~~~ \Phi_\epsilon~=~\frac{\kappa z}{u_*^3}\epsilon \]

a) Find the non-dimensional equation for TKE at the surface layer in terms of \(\Phi_M\), \(\Phi_\epsilon\) and \(z/L\).

Hint

• Assume that we look at the surface layer (where turbulent fluxes are relatively constant on height and vary less than 10%), so \(\overline{u'w'} \approx \overline{u'w'}_0 = -u_*^2\). Also \(\overline{w'\theta_v'} \approx \overline{w'\theta_v'}_0\).

• Remember that the Monin-Obukhov length is defined by

\[ L = \frac{-\overline{\theta_v}\,u_*^3}{\kappa\,g\,\overline{w'\theta_v'}_0}, \]

Answer

To make the TKE equation more general for boundary layer statistics, everything is scaled. Typical measures for momentum and dissipation are

\[\begin{split} \Phi_m &= \frac{\kappa\, z}{u_*}\gemafg{u}{z}\\ \Phi_\epsilon &= \frac{\kappa\, z}{u_*^3}\epsilon \end{split}\]

This can be rewritten to

(19.4)\[ \gemafg{u}{z} = \Phi_m \frac{u_*}{\kappa\, z} \]

(19.5)\[ \epsilon = \Phi_\epsilon \frac{u_*^3}{\kappa\, z} \]

Substituting Equations (19.4) and (19.5) in Equation (19.3), yields

\[ 0= -\overline{u'w'}\frac{u_*\Phi_m}{\kappa \,z} + \frac{g}{\overline{\theta_v}}\overline{w'\theta_v'} - \frac{u_*^3 \Phi_\epsilon}{\kappa\, z} \]

Since the \(\Phi_{m}\) and \(\Phi_{\epsilon}\) are dimensionless, the units of the total equation are \(\rm m^2\,s^{-3}\). How to make this equation dimensionless? The last term shows, an easy way is to multiply the whole equation by \(\frac{\kappa z}{u_*^3}\), which results in

\[ 0= \frac{-\overline{u'w'}}{u_*^2}\Phi_m + \frac{\kappa\,g\,\overline{w'\theta_v'}}{\overline{\theta_v}\,u_*^3}z - \Phi_\epsilon \]

We look at the surface layer, so \(\overline{u'w'} \approx \overline{u'w'}_0 = -u_*^2\). Also \(\overline{w'\theta_v'} \approx \overline{w'\theta_v'}_0\).

Considering that the Monin-Obukhov length is defined by

\[ L = \frac{-\overline{\theta_v}\,u_*^3}{\kappa\,g\,\overline{w'\theta_v'}_0}, \]

the total TKE equation can be rewritten to \(0=\Phi_m-\frac{z}{L}-\Phi_\epsilon\)

b) Discuss the relative importance of buoyancy, shear and dissipation under neutral conditions.

Answer

Under neutral stratifying conditions, \(\frac{z}{L}=0\) (since the buoyancy flux is 0). Therefore, what remains of the TKE equation is \(\Phi_m=\Phi_\epsilon\). All kinetic energy that is generated by shear is directly dissipated.

Note that we came to the same conclusion with a less formal derivation in exercise 1.